Численные методы анализа и синтеза периодических сигналов

Численные методы анализа и синтеза периодических сигналов

Численные методы анализа и синтеза периодических сигналов Содержание:

Введение

1. Спектральный анализ и спектральный синтез периодических сигналов

1.1 Синтез периодических сигналов

1.2 Анализ периодических сигналов

2.Численные методы расчетов спектральных и временных характеристик периодических сигналов

2.1 Численные методы расчетов временных характеристик

2.2.Численные методы расчетов частотных характеристик

Выводы

Литература

Введение:

Известно , что периодическое несинусоидальное колебание можно представить бесконечным тригонометрическим рядом Фурье, который в общем случае содержит постоянную и гармонические составляющие .

Часто используется следующая форма математической записи ряда Фурье:

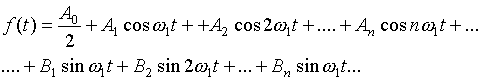
где f(t)-функция, раскладываемая в ряд,

, а - частота следования импульсов.

Коэффициенты ряда определяются следующими выражениями:

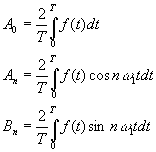(1)

где =1,2,3…M соответственно функции(1.2),(1.3),(1.4)

Здесь А - постоянная составляющая , An и Bn - амплитуды косинусной и синусной составляющих, Т- период повторения сигнала , М- число гармоник,

n – номер гармоник. Ряд (1) можно преобразовать к более удобному виду:

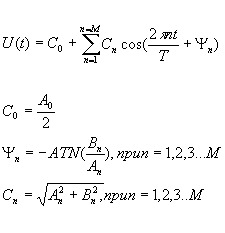(2)

Здесь -постоянная составляющая, -амплитуда n-ой гармоники,-фаза n-ой гармоники. Формула (2.1) используется при спектральном анализе и синтезе периодических сигналов.

1.Спектральный анализ и спектральный синтез периодических сигналов 1.1. СПЕКТРАЛЬНЫЙ СИНТЕЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ:

Сигнал задан в виде набора спектральных составляющих: Cn – амплитуда,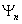- частота,

начальная фаза n- ой гармоники. Здесь n=1,2,…,M- номер гармоники , M- число гармоник в спектре сигналов. Требуется осуществить синтез сигнала U(t) и построить его временную диаграмму. Задача синтеза сигнала заключается в расчёте временной функции сигнала U(t) по известному спектру сигнала. При этом спектр сигнала задан в виде таблицы амплитуд, частот и фаз гармоник. Задача синтеза сигнала решается путём расчёта значений функции во временной области U(t)

Численный синтез осуществляется путём расчёта отсчетов сигнала через равные интервалы времени и построения временной диаграммы сигнала. При этом интервал времени между соседними отсчётами называют интервалом дискретизации.

1.2СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ:

Задача анализа сигнала заключается в расчёте его спектра, т.е. амплитуд, частот, фаз и гармоник. При этом сигнал задан в виде функции времени U(t) . Задача анализа решается путём расчёта амплитудно-частотных Cn=f(w) и фазочастотных =f(w) характеристик.

Сигнал задан в виде функции времени U(t) , повторяющийся с периодом Т. Требуется выполнить спектральный анализ сигнала и построить графики амплитудного и фазового спектров сигнала.

2.Численные методы расчетов спектральных и временных характеристик периодических сигналов

Для расчета спектральных и временных характеристик периодического сигнала используем численные методы, чтобы упростить и автоматизировать задачу

Дан сигнал:

Дана таблица параметров данного сигнала

U, mv Наш опрос Как Вы оцениваете работу нашего сайта? Отлично Не помог Результаты опроса Реклама   Мнение авторов может не совпадать с мнением редакции сайта Перепечатка материалов без ссылки на наш сайт запрещена